Bezier 曲线曲面绘制

Bernstein 基函数

在 Weierstrass 第一定理的构造性证明中，证明的关键是利用 Bernstein 基函数. 下面将介绍 Bernstein 基函数在计算几何中的应用，这类基函数具有“几何直观”的优良性质.

n 次多项式 Bernstein 基函数为

其中

举例：时，三次 Bernstein 多项式为

对应图形如图所示.

基本性质

• 非负性.
• 单位分解性.
• 端点性质. 在端点，分别只有一个 Bernstein 基函数取值为 1，其余全部为 0，即

• 对称性.

• 递推公式. 每一个 n 次 Bernstein 基函数可以由两个 n-1 次 Bernstein 基函数递推得到，即

• 最大值. 时，Bernstein 基函数在处取得唯一最大值.

• 积分等值性. 所有 n 次 Bernstein 基函数在上积分值相等.

Bezier 曲线

定义

称参数曲线段

为一条 n 次Bezier 曲线，其中为 n 次 Bernstein 基函数，空间向量**称为控制顶点，依次用直线段连接相邻两个控制顶点得到的 n 边折线多边形称为控制多边形.**

实例代码

对于控制顶点

平面上的三次 Bezier 曲线方程为

x=[0,1,2,3];
y=[0,2,-1,1];
n=length(x)-1;
xx=0;yy=0;
syms t
for k=0:n
    B=nchoosek(n,k)*t^k*(1-t)^(n-k);
    xx=xx+x(k+1)*B;
    yy=yy+y(k+1)*B;
end
xx=collect(xx);
yy=collect(yy);
fprintf('三次Bezier曲线方程为：x(t)=%s,y(t)=%s\n',xx,yy);
t1=linspace(0,1);
xx1=subs(xx,t,t1);
yy1=subs(yy,t,t1);
figure();
plot(x,y,'g*','markersize',10);
line(x,y,'color',[0 0 1])
hold on
plot(xx1,yy1,'r-')
hold off

控制顶点用绿色*标注，控制多边形设置为蓝色，Bezier 曲线为红色，结果如图所示.

张量积型 Bernstein 基函数

对 m 次与 n 次一元 Bernstein 基函数

张量积型次二元 Bernstein 基函数为

这个多项式线性无关，从而构成二元多项式空间的一组基.

Bezier 曲面

定义

参数曲面

为次 Bezier 曲面，其中为张量积型 Bernstein 基函数，空间向量称为控制顶点，依次用直线段连接同行同列相邻两个控制顶点得到边折线网格称为控制网格.

实例代码

对于给定控制顶点

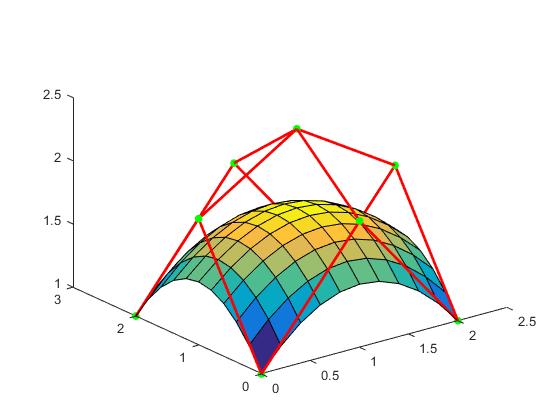
绘制次 Bezier 曲面

%控制顶点
Px=[0,0,0;1,1,1;2,2,2];
Py=[0,1,2;0,1,2;0,1,2];
Pz=[1,2,1;2,2.5,2;1,2,1];
figure();
plot3(Px,Py,Pz,'r','linewidth',2);
hold on
plot3(Px',Py',Pz','r','linewidth',2);
hold on
plot3(Px,Py,Pz,'g.','markersize',20,'linewidth',2);
hold on
a=0;b=1;
N=10;M=10;
hx=(b-a)/N;
hy=(b-a)/M;
x=(a:hx:b)';
y=(a:hy:b)';
n=2;m=2;
[x,y]=meshgrid(x,y);
PX=zeros(N+1,M+1);
PY=zeros(N+1,M+1);
PZ=zeros(N+1,M+1);
for i=1:n+1
    for j=1:m+1
        PX=PX+Px(i,j)*nchoosek(n,i-1).*(x.^(i-1)).*((1-x).^(n-i+1)).*nchoosek(n,j-1).*(y.^(j-1)).*((1-y).^(n-j+1));
        PY=PY+Py(i,j)*nchoosek(n,i-1).*(x.^(i-1)).*((1-x).^(n-i+1)).*nchoosek(n,j-1).*(y.^(j-1)).*((1-y).^(n-j+1));
        PZ=PZ+Pz(i,j)*nchoosek(n,i-1).*(x.^(i-1)).*((1-x).^(n-i+1)).*nchoosek(n,j-1).*(y.^(j-1)).*((1-y).^(n-j+1));
    end
end
surf(PX,PY,PZ)

控制顶点用绿色点标注，控制网格设置为红色，结果如图所示.