平衡二叉树

平衡树

平衡树（Balanced Tree）是一种特殊的二叉搜索树：

其目的是通过一些特殊的技巧来维护树的高度平衡
从而保证树的搜索、插入、删除等操作的时间复杂度都较低

为什么需要平衡树呢?

如果一棵树退化成链状结构，那么搜索、插入、删除等操作的时间复杂度就会达到最坏情况，即 O(n)，因此不能满足要求
平衡树通过不断调整树的结构，使得树的高度尽量平衡，从而保证搜索、插入、删除等操作的时间复杂度都较低，通常为 O(logn)
因此，如果我们需要高效地处理大量的数据，那么平衡树就显得非常重要了

平衡树的应用非常广泛，如索引、内存管理、图形学等领域均有广泛使用

事实上不只是添加会导致树的不平衡，删除元素也可能会导致树的不平衡

如何让树更加平衡

方式一：限制插入、删除的节点（比如在树特性的状态下，不允许插入或者删除某些节点，不现实）

方式二：在随机插入或者删除元素后，通过某种方式观察树是否平衡，如果不平衡通过特定的方式（比如旋转），让树保持平衡

平衡二叉搜索树

AVL树：这是一种最早的平衡二叉搜索树，在 1962 年由 GM.Adelson-Velsky 和 E.M.Landis 发明
红黑树：这是一种比较流行的平衡二叉搜索树，由 R.Bayer 在 1972 年发明
Splay树：这是一种动态平衡二叉搜索树，通过旋转操作对树进行平衡
Treap：这是一种随机化的平衡二叉搜索树，是二叉搜索树和堆的结合
B-树：这是一种适用于磁盘或其他外存存储设备的多路平衡查找树

这些平衡二又搜索树都用于保证搜索树的平衡，从而在插入、删除、查找操作时保证了较低的时间复杂度

红黑树和AVL树是应用最广泛的平衡二又搜索树:

红黑树：红黑树被广泛应用于实现诸如操作系统内核、数据库、编译器等软件中的数据结构，其原因在于它在插入、删除、查找操作时都具有较低的时间复杂度
AVL树：AVL树被用于实现各种需要高效查询的数据结构，如计算机图形学、数学计算和计算机科学研究中的一些特定算法

AVL树

AVL树 (Adelson-Velsky and Landis Tree) 是由 G.M.Adelson-Velsky 和 E.M.Landis 在 1962 年发明的

它是一种自（Self）平衡二叉搜索树
它是二叉搜索树的一个变体，在保证二叉搜索树性质的同时，通过旋转操作保证树的平衡

在AVL树中，每个节点都有一个权值，该权值代表了以该节点为根节点的子树的高度差

在AVL树中，任意节点的权值只有 1 或 -1 或 0，因此AVL树也被称为高度平衡树
对于每个节点，它的左子树和右子树的高度差不超过1
这使得AVL树具有比普通的二叉搜索树更高的查询效率
当插入或删除节点时，AVL树可以通过旋转操作来重新平衡树，从而保证其平衡性

AVL树的插入和删除操作与普通的二叉搜索树类似，但是在插入或者删除之后，需要继续保持树的平衡

AVL树需要通过旋转操作来维护平衡
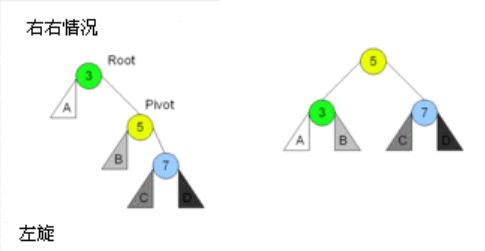
有四种情况旋转操作：左左情况、右右情况、左右情况和右左情况双旋口
具体使用哪一种旋转，要根据不同的情况来进行区分和判断

由于AVL树具有自平衡性，因此其最坏情况下的时间复杂度仅 O(log n)

旋转情况

此动画演示了不断将节点插入AVL树时的情况，并且演示了左旋（Left Rotation）、右旋（Right Rotation）、右左旋转（Right-Left Rotation）、左右旋转（Left-Right Rotation）以及带子树的右旋（Right Rotation with children）

AVL_Tree_Example

以下图表以四列表示四种情况，每行表示在该种情况下要进行的操作。在左左和右右的情况下，只需要进行一次旋转操作；在左右和右左的情况下，需要进行两次旋转操作

如下图片来自维基百科

如何对 AVL 树进行旋转呢？

首先，我们需要先找到失衡的节点：

失衡的节点称之为 grandParent
失衡节点的儿子(更高的儿子)称之为 parent
失衡节点的孙子(更高的孙子)称之为 current

如果从 grandParent 到 current 的是：

LL：左左情况，那么右旋转
RR：右右情况，那么左旋转
LR：左右情况，那么先对 parent 进行左旋转，再对 grandParent 进行右旋转
RL：右左情况，那么先对 parent 进行右旋转，再对 grandParent 进行左旋转

封装过程

手写实现AVL树本身的过程是相当的复杂的，最好是分而治之，最好分为如下五步

步骤一：AVL树节点的封装
步骤二：AVL树的旋转情况
步骤三：不同情况下进行的不同旋转操作
步骤四：插入操作后，树的再平衡操作
步骤五：删除操作后，树的再平衡操作

grand/root -> parent/pivot -> current

树节点封装

封装 AVLTreeNode 类，有判断平衡获取更高子节点等方法

typescript

import { TreeNode } from './TreeNode'

class AVLTreeNode<T> extends TreeNode<T> {
  left: AVLTreeNode<T> | null = null
  right: AVLTreeNode<T> | null = null
  parent: AVLTreeNode<T> | null = null

  height: number = 1
  /** 获取每个节点的高度 */
  getHeight(): number {
    const leftHeight = this.left ? this.left.getHeight() : 0
    const rightHeight = this.right ? this.right.getHeight() : 0
    return Math.max(leftHeight, rightHeight) + 1
  }
  /** 权重：平衡因子（左height - 右height） */
  getBalanceFactor(): number {
    const leftHeight = this.left ? this.left.getHeight() : 0
    const rightHeight = this.right ? this.right.getHeight() : 0
    return leftHeight - rightHeight
  }
  /** 直接判断当前节点是否平衡 */
  get isBalanced(): boolean {
    const factor = this.getBalanceFactor()
    return Math.abs(factor) <= 1
  }
  /** 获取更高子节点 */
  public get higherChild(): AVLTreeNode<T> | null {
    const leftHeight = this.left ? this.left.getHeight() : 0
    const rightHeight = this.right ? this.right.getHeight() : 0
    if (leftHeight > rightHeight) return this.left
    if (leftHeight < rightHeight) return this.right
    return this.isLeft ? this.left : this.right
  }
}

右旋转

最核心的是找到不平衡的节点，之后从上向下去分析：LL/LR/RR/RL

root 节点的 left 造成的不平衡，之后找到 pivot 节点，它也是 left 造成的不平衡，所以是 left left(LL)情况

bash

   (root)5
        / \
(pivot)3   A    右旋转 ->    3
      / \                 /   \
     2   B               2     5
    / \                 / \   / \
   D   C               D   C B   A

实现步骤分析：

处理 pivot 的位置

选择当前节点的左子节点作为旋转轴心(pivot)
pivot 的父节点指向 root 当前节点的父节点
typescript
```
const pivot = root.left
pivot.parent = root.parent
```
1
2

处理 pivot 右节点的位置

root 当前节点的左节点

如果父节点有值，那么右节点的父节点指向 root 节点

typescript

root.left = pivot.right
if (pivot.right) {
  pivot.right.parent = root
}
pivot.right = root

处理 root 节点的位置

pivot 的右节点指向 root
root 节点父节点指向 pivot
typescript
```
pivot.right = root
root.parent = pivot
```
1
2

判断是否有父节点，父节点的 left/right 指向 pivot

typescript

// 情况一：pivot.parent 为 null/undefined
avltree.root = pivot
// 情况二：父节点的左子节点
pivot.parent.left = pivot
// 情况三：pivot 是父节点的右子节点
pivot.parent.right = pivot

typescript

class AVLTreeNode<T> extends TreeNode<T> {
  /** 旋转操作：右旋转 */
  rightRotation() {
    const isLeft = this.isLeft
    const isRight = this.isRight
    // 1.处理pivot节点
    const pivot = this.left!
    pivot.parent = this.parent
    // 2.处理pivot的right
    this.left = pivot.right
    if (pivot.right) {
      pivot.right.parent = this
    }
    // 3.处理root
    pivot.right = this
    this.parent = pivot
    // 4.挂载pivot
    if (!pivot.parent) {
      // pivot直接作为tree的根
      return pivot
    } else if (isLeft) {
      // pivot作为父节点的左子节点
      pivot.parent.left = pivot
    } else if (isRight) {
      // pivot作为父节点的右子节点
      pivot.parent.right = pivot
    }
    return pivot
  }
}

// 测试用例
const avlNode = new AVLTreeNode(10)
avlNode.left = new AVLTreeNode(8)
avlNode.left.parent = avlNode
avlNode.left.left = new AVLTreeNode(5)
avlNode.left.left.parent = avlNode.left
const parent = new AVLTreeNode(12)
avlNode.parent = parent
parent.left = avlNode
btPrint(parent)
avlNode.rightRotation()
btPrint(parent)

左旋转

根右旋转结构一致，只是需要处理 left 情况了

typescript

class AVLTreeNode<T> extends TreeNode<T> {
  /** 旋转操作：左旋转 */
  leftRotation() {
    const isLeft = this.isLeft
    const isRight = this.isRight
    // 1.处理pivot
    const pivot = this.right!
    pivot.parent = this.parent
    // 2.处理pivot的left
    this.right = pivot.left
    if (pivot.left) {
      pivot.left.parent = this
    }
    // 3.处理root
    pivot.left = this
    this.parent = pivot
    // 4.挂载pivot
    if (!pivot.parent) {
      return pivot
    } else if (isLeft) {
      pivot.parent.left = pivot
    } else if (isRight) {
      pivot.parent.right = pivot
    }
    return pivot
  }
}

// 测试用例
const avlNode = new AVLTreeNode(10)
avlNode.right = new AVLTreeNode(15)
avlNode.right.parent = avlNode
avlNode.right.right = new AVLTreeNode(20)
avlNode.right.right.parent = avlNode.right
const parent = new AVLTreeNode(6)
avlNode.parent = parent
parent.right = avlNode
btPrint(parent)
avlNode.leftRotation()
btPrint(parent)

再平衡

这里又封装了一个类 AVLTree，继承 BSTree，这样就有 insert 等方法了，reBalance 方法里接收一个 AVLTreeNode 实例，这样也可以调用左旋转右旋转方法

typescript

class AVLTree<T> extends BSTree<T> {
  /**
   * 根据不平衡的节点的情况(LL/LR/RL/RR)
   * @param root 找到不平衡的节点
   */
  reBalance(root: AVLTreeNode<T>) {
    const pivot = root.higherChild
    const current = pivot?.higherChild
    let resultNode: AVLTreeNode<T> | null = null
    if (pivot?.isLeft) {
      if (current?.isLeft) {
        // LL
        resultNode = root.rightRotation()
      } else {
        // LR
        pivot.leftRotation()
        resultNode = root.rightRotation()
      }
    } else {
      if (current?.isLeft) {
        // RL
        pivot?.rightRotation()
        resultNode = root.leftRotation()
      } else {
        // RR
        resultNode = root.leftRotation()
      }
    }
    // 判断返回的 pivot 是否有父节点
    if (!resultNode.parent) {
      this.root = resultNode
    }
  }
}

插入细节调整

现在插入还是不会做平衡操作，插入的时候(BSTree 类)做了如下操作

按照默认二叉搜索树插入，创建的节点是 TreeNode 而不是 AVLTreeNode，这里就会有问题，这里思考一下如何处理？

insert 使可以让别人传入一个类，但是麻烦很多且使用时传入一个类很怪异

现在父类实现 createNode 模板方法，如果子类对这个方法有额外需求，在子类重写这个方法即可

typescript

export class BSTree<T> {
  protected createNode(value: T): TreeNode<T> {
    return new TreeNode(value)
  }
  insert(value: T) {
    // 1.根据传入value创建Node(TreeNode)节点
    const newNode = this.createNode(value)
    // 2.判断当前是否已经有了根节点
    if (!this.root) {
      // 当前树为空
      this.root = newNode
    } else {
      // 树中已经有其他值
      this.insertNode(this.root, newNode)
    }
  }
}

class AVLTree<T> extends BSTree<T> {
  protected createNode(value: T): TreeNode<T> {
    return new AVLTreeNode(value)
  }
}

之后再在 insertNode 进行重构，给每个 node 节点增加 parent，AVL 树需要知道父节点，BST 树无需知道父节点。之后在插入后增加检查树是否平衡操作，父类无需实现这个方法，让子类来实现

typescript

export class BSTree<T> {
  protected checkBalance(node: TreeNode<T>) {}
  insert(value: T) {
    // 1.根据传入value创建Node(TreeNode)节点
    const newNode = this.createNode(value)
    // 2.判断当前是否已经有了根节点
    if (!this.root) {
      // 当前树为空
      this.root = newNode
    } else {
      // 树中已经有其他值
      this.insertNode(this.root, newNode)
    }
    // 3.检查树是否平衡
    this.checkBalance(newNode)
  }
  private insertNode(node: TreeNode<T>, newNode: TreeNode<T>) {
    if (newNode.data < node.data) {
      // 去左边继续查找空白位置
      if (node.left === null) {
        node.left = newNode
        newNode.parent = node
      } else {
        this.insertNode(node.left, newNode)
      }
    } else {
      // 去右边继续查找空白位置
      if (node.right === null) {
        node.right = newNode
        newNode.parent = node
      } else {
        this.insertNode(node.right, newNode)
      }
    }
  }
}

子类实现 checkBalance 方法

typescript

class AVLTree<T> extends BSTree<T> {
  // 如果去找到不平衡的节点
  checkBalance(node: AVLTreeNode<T>) {
    let current = node.parent
    while (current) {
      if (!current.isBalanced) {
        this.reBalance(current)
      }
      current = current.parent
    }
  }
}

测试用例进行检查

typescript

const avlTree = new AVLTree<number>()
for (let i = 0; i < 20; i++) {
  avlTree.insert(Math.floor(Math.random() * 200))
}
avlTree.print()

AVL树完整代码

BSTree

typescript

import { btPrint } from 'hy-algokit'

export class Node<T> {
  data: T
  constructor(value: T) {
    this.data = value
  }
}
export class TreeNode<T> extends Node<T> {
  left: TreeNode<T> | null = null
  right: TreeNode<T> | null = null
  parent: TreeNode<T> | null = null
  get value() {
    return this.data
  }
  get isLeft(): boolean {
    return !!(this.parent && this.parent.left === this)
  }
  get isRight(): boolean {
    return !!(this.parent && this.parent.right === this)
  }
}

export class BSTree<T> {
  protected root: TreeNode<T> | null = null
  print() {
    btPrint(this.root)
  }
  private searchNode(value: T): TreeNode<T> | null {
    let current = this.root
    let parent: TreeNode<T> | null = null
    while (current) {
      if (current.data === value) return current
      parent = current
      if (current.data < value) {
        current = current.right
      } else {
        current = current.left
      }
      if (current) current.parent = parent
    }
    return null
  }
  protected createNode(value: T): TreeNode<T> {
    return new TreeNode(value)
  }
  protected checkBalance(node: TreeNode<T>, isAdd?: boolean) {}
  /** 插入数据的操作 */
  insert(value: T) {
    // 1.根据传入value创建Node(TreeNode)节点
    const newNode = this.createNode(value)
    // 2.判断当前是否已经有了根节点
    if (!this.root) {
      // 当前树为空
      this.root = newNode
    } else {
      // 树中已经有其他值
      this.insertNode(this.root, newNode)
    }
    // 3.检查树是否平衡
    this.checkBalance(newNode)
  }
  private insertNode(node: TreeNode<T>, newNode: TreeNode<T>) {
    if (newNode.data < node.data) {
      // 去左边继续查找空白位置
      if (node.left === null) {
        node.left = newNode
        newNode.parent = node
      } else {
        this.insertNode(node.left, newNode)
      }
    } else {
      // 去右边继续查找空白位置
      if (node.right === null) {
        node.right = newNode
        newNode.parent = node
      } else {
        this.insertNode(node.right, newNode)
      }
    }
  }
  /** 遍历的操作 */
  /** 先序遍历 */
  preOrderTraverse() {
    this.preOrderTraverseNode(this.root)
  }
  private preOrderTraverseNode(node: TreeNode<T> | null) {
    if (node) {
      console.log(node.data)
      this.preOrderTraverseNode(node.left)
      this.preOrderTraverseNode(node.right)
    }
  }
  preOrderTraversalNoRecursion() {
    let stack: TreeNode<T>[] = []
    let current: TreeNode<T> | null = this.root
    while (current !== null || stack.length !== 0) {
      while (current !== null) {
        console.log(current.data)
        stack.push(current)
        current = current.left
      }
      current = stack.pop()!
      current = current.right
    }
  }
  /** 中序遍历 */
  inOrderTraverse() {
    this.inOrderTraverseNode(this.root)
  }
  private inOrderTraverseNode(node: TreeNode<T> | null) {
    if (node) {
      this.inOrderTraverseNode(node.left)
      console.log(node.data)
      this.inOrderTraverseNode(node.right)
    }
  }
  inOrderTraversalNoRecursion() {
    let stack: TreeNode<T>[] = []
    let current: TreeNode<T> | null = this.root
    while (current !== null || stack.length !== 0) {
      while (current !== null) {
        stack.push(current)
        current = current.left
      }
      current = stack.pop()!
      console.log(current.data)
      current = current.right
    }
  }
  /** 后序遍历 */
  postOrderTraverse() {
    this.postOrderTraverseNode(this.root)
  }
  private postOrderTraverseNode(node: TreeNode<T> | null) {
    if (node) {
      this.postOrderTraverseNode(node.left)
      this.postOrderTraverseNode(node.right)
      console.log(node.data)
    }
  }
  postOrderTraversalNoRecursion() {
    let stack: TreeNode<T>[] = []
    let current: TreeNode<T> | null = this.root
    let lastVisitedNode: TreeNode<T> | null = null
    while (current !== null || stack.length !== 0) {
      while (current !== null) {
        stack.push(current)
        current = current.left
      }
      current = stack[stack.length - 1]
      if (current.right === null || current.right === lastVisitedNode) {
        console.log(current.data)
        lastVisitedNode = current
        stack.pop()
        current = null
      } else {
        current = current.right
      }
    }
  }
  /** 层序遍历 */
  levelOrderTraverse() {
    // 1.如果没有根节点，那么不需要遍历
    if (!this.root) return
    // 2.创建队列结构
    const queue: TreeNode<T>[] = []
    queue.push(this.root)
    // 3.遍历队列中所有的节点（依次出队）
    while (queue.length) {
      // 3.1访问节点的过程
      const current = queue.shift()!
      console.log(current.data)
      // 3.2将左子节点放入队列
      if (current.left) {
        queue.push(current.left)
      }
      // 3.3将右子节点放入到队列
      if (current.right) {
        queue.push(current.right)
      }
    }
  }
  /** 获取最值操作：最大值 */
  getMaxValue(): T | null {
    let current = this.root
    while (current && current.right) {
      current = current.right
    }
    return current?.data ?? null
  }
  /** 获取最值操作：最小值 */
  getMinValue(): T | null {
    let current = this.root
    while (current && current.left) {
      current = current.left
    }
    return current?.data ?? null
  }
  /** 搜索特定的值 */
  searchNoRecursion(value: T): boolean {
    let current = this.root
    while (current) {
      // 找到了节点
      if (current.data === value) return true
      if (current.data < value) {
        current = current.right
      } else {
        current = current.left
      }
    }
    return false
  }
  search(value: T): boolean {
    return !!this.searchNode(value)
  }
  searchNodeValue(node: TreeNode<T> | null, value: T): boolean {
    // 1.如果节点为null，那么就直接退出递归
    if (node === null) return false
    // 2.判断node节点的value和传入的value的大小
    if (node.data > value) {
      return this.searchNodeValue(node.left, value)
    } else if (node.data < value) {
      return this.searchNodeValue(node.right, value)
    } else {
      return true
    }
  }
  /** 删除操作 */
  private getSuccessor(delNode: TreeNode<T>) {
    // 获取右子树
    let current = delNode.right
    let successor: TreeNode<T> | null = null
    while (current) {
      successor = current
      current = current.left
      if (current) {
        current.parent = successor
      }
    }
    // 拿到后继节点
    if (successor !== delNode.right) {
      successor!.parent!.left = successor!.right
      successor!.right = delNode.right
      if (successor?.right) {
        successor.right.parent = successor.parent
      }
    } else {
      delNode.right = successor!.right
      if (successor!.right) {
        successor!.right.parent = delNode
      }
    }

    // 将删除节点的 left，赋值给后继节点的 left
    successor!.left = delNode.left
    return successor!
  }
  remove(value: T): boolean {
    // 1.搜索当前是否有这个value
    const current = this.searchNode(value)
    if (!current) return false

    let delNode: TreeNode<T> = current
    // 2.获取到三个东西：当前节点/父节点是否属于父节点的左子节点还是右子节点
    let replaceNode: TreeNode<T> | null = null
    if (current.left === null && current.right === null) {
      // 2.1.如果删除的是叶子节点
      replaceNode = null
    } else if (current.right === null) {
      // 2.2.只有一个子节点，只有左子节点
      replaceNode = current.left
    } else if (current.left === null) {
      // 2.3.只有一个子节点，只有右子节点
      replaceNode = current.right
    } else {
      // 2.4.两个子节点
      const successor = this.getSuccessor(current)
      // replaceNode = successor
      current.data = successor.data
      delNode = successor
      replaceNode = current
      this.checkBalance(delNode)
      return true
    }
    if (current === this.root) {
      this.root = replaceNode
    } else if (current.isLeft) {
      current.parent!.left = replaceNode
    } else {
      current.parent!.right = replaceNode
    }
    if (replaceNode && current.parent) {
      replaceNode.parent = current.parent
    }
    // 删除完成后，检测数是否平衡(传入的节点是那个真正从二叉树被移除的节点)
    this.checkBalance(delNode, false)
    return true
  }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300

AVLTreeNode

typescript

import { TreeNode } from './BSTree'

export default class AVLTreeNode<T> extends TreeNode<T> {
  left: AVLTreeNode<T> | null = null
  right: AVLTreeNode<T> | null = null
  parent: AVLTreeNode<T> | null = null

  height: number = 1
  /** 获取每个节点的高度 */
  getHeight(): number {
    const leftHeight = this.left ? this.left.getHeight() : 0
    const rightHeight = this.right ? this.right.getHeight() : 0
    return Math.max(leftHeight, rightHeight) + 1
  }
  /** 权重：平衡因子（左height - 右height） */
  getBalanceFactor(): number {
    const leftHeight = this.left ? this.left.getHeight() : 0
    const rightHeight = this.right ? this.right.getHeight() : 0
    return leftHeight - rightHeight
  }
  /** 直接判断当前节点是否平衡 */
  get isBalanced(): boolean {
    const factor = this.getBalanceFactor()
    return Math.abs(factor) <= 1
  }
  /** 获取更高子节点 */
  public get higherChild(): AVLTreeNode<T> | null {
    const leftHeight = this.left ? this.left.getHeight() : 0
    const rightHeight = this.right ? this.right.getHeight() : 0
    if (leftHeight > rightHeight) return this.left
    if (leftHeight < rightHeight) return this.right
    return this.isLeft ? this.left : this.right
  }
  /** 旋转操作：右旋转 */
  rightRotation() {
    const isLeft = this.isLeft
    const isRight = this.isRight
    // 1.处理pivot节点
    const pivot = this.left!
    pivot.parent = this.parent
    // 2.处理pivot的right
    this.left = pivot.right
    if (pivot.right) {
      pivot.right.parent = this
    }
    // 3.处理root
    pivot.right = this
    this.parent = pivot
    // 4.挂载pivot
    if (!pivot.parent) {
      // pivot直接作为tree的根
      return pivot
    } else if (isLeft) {
      // pivot作为父节点的左子节点
      pivot.parent.left = pivot
    } else if (isRight) {
      // pivot作为父节点的右子节点
      pivot.parent.right = pivot
    }
    return pivot
  }
  /** 旋转操作：左旋转 */
  leftRotation() {
    const isLeft = this.isLeft
    const isRight = this.isRight
    // 1.处理pivot
    const pivot = this.right!
    pivot.parent = this.parent
    // 2.处理pivot的left
    this.right = pivot.left
    if (pivot.left) {
      pivot.left.parent = this
    }
    // 3.处理root
    pivot.left = this
    this.parent = pivot
    // 4.挂载pivot
    if (!pivot.parent) {
      return pivot
    } else if (isLeft) {
      pivot.parent.left = pivot
    } else if (isRight) {
      pivot.parent.right = pivot
    }
    return pivot
  }
}

AVLTree

typescript

import AVLTreeNode from './AVLTree4-左旋转'
import { BSTree, TreeNode } from './TreeNode'

class AVLTree<T> extends BSTree<T> {
  protected createNode(value: T): TreeNode<T> {
    return new AVLTreeNode(value)
  }
  // 如果去找到不平衡的节点
  checkBalance(node: AVLTreeNode<T>, isAdd = true) {
    let current = node.parent
    while (current) {
      if (!current.isBalanced) {
        this.reBalance(current)
        // 这个位置是旋转完成后的操作
        // break 决定不会进一步去查找父节点有没有平衡的情况
        // 添加的情况是不需要进一步向上查找的，直到 break
        // 删除的情况是需要进一步向上查找的，不能 break
        if (isAdd) break
      }
      current = current.parent
    }
  }

  // 假设已经找到了，那么我们如何让这个节点变的不平衡
  /**
   * 根据不平衡的节点的情况(LL/LR/RL/RR)
   * @param root 找到不平衡的节点
   */
  reBalance(root: AVLTreeNode<T>) {
    const pivot = root.higherChild
    const current = pivot?.higherChild
    let resultNode: AVLTreeNode<T> | null = null
    if (pivot?.isLeft) {
      if (current?.isLeft) {
        // LL
        resultNode = root.rightRotation()
      } else {
        // LR
        pivot.leftRotation()
        resultNode = root.rightRotation()
      }
    } else {
      if (current?.isLeft) {
        // RL
        pivot?.rightRotation()
        resultNode = root.leftRotation()
      } else {
        // RR
        resultNode = root.leftRotation()
      }
    }
    // 判断返回的 pivot 是否有父节点
    if (!resultNode.parent) {
      this.root = resultNode
    }
  }
}

const avlTree = new AVLTree<number>()
const delNumber: number[] = []
for (let i = 0; i < 16; i++) {
  const randomNum = Math.floor(Math.random() * 200)
  if (i % 2 === 0 && delNumber.length < 8) {
    delNumber.push(randomNum)
  }
  avlTree.insert(randomNum)
}
avlTree.print()

for (const delNum of delNumber) {
  avlTree.remove(delNum)
}
avlTree.print()

平衡二叉树 ​

平衡树 ​

如何让树更加平衡 ​

平衡二叉搜索树 ​

AVL树 ​

旋转情况 ​

封装过程 ​

树节点封装 ​

右旋转 ​

左旋转 ​

再平衡 ​

插入细节调整 ​

AVL树完整代码 ​

BSTree ​

AVLTreeNode ​

AVLTree ​

平衡二叉树

平衡树

如何让树更加平衡

平衡二叉搜索树

AVL树

旋转情况

封装过程

树节点封装

右旋转

左旋转

再平衡

插入细节调整

AVL树完整代码

BSTree

AVLTreeNode

AVLTree